先日、極座標のマテリアル構成について記事にしました。
その中でタンジェントの逆三角関数であるアークタンジェントとFracを使ってUVを極座標展開している部分について補足したいと思います。
まず、該当する構成がこちら。綺麗に円状にグラデーションができてますね。
UV座標＞UV座標の範囲を補正＞Arctangent2＞Divide＞Fracといった流れになっています。
順にみていきます。
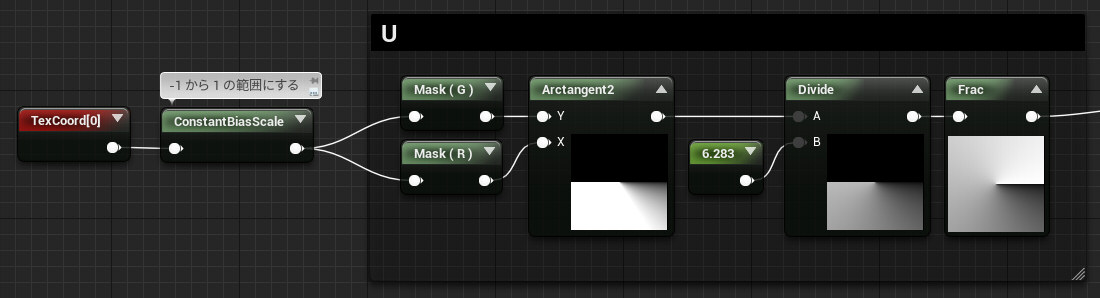
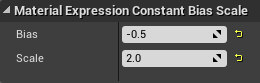
まず最初に、UV座標を ConstantBiasScale で「-1～1」の範囲に広げています。
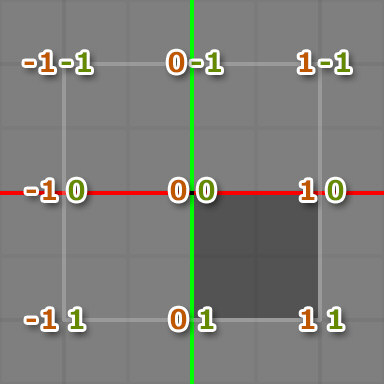
下図のようなイメージです。Vは下方向がプラスなのでご注意。
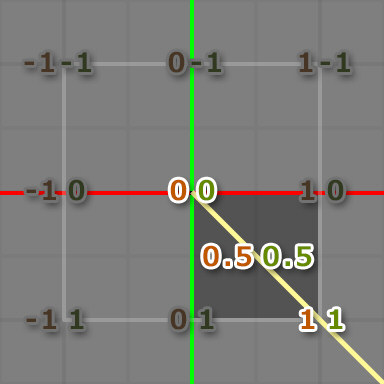
そしてArctangent2ノードに繋いでいる訳ですが、そもそも「アークタンジェントは何か？」と言えば「XとYの比率 () から角度を求める」ことができる便利な関数です。
原点から放射状に線を伸ばすと、直線状のどこに注目しても、XとY (UとV) の比率は変わらないし角度も同じですよね。下図で言えば、0.5, 0.5 でも 1, 1 でも 2, 2 でも45度な訳です。
そして、Arctangentの関数は「atan」と「atan2」の2種類あります。
atan2は X と Y の2つの値を入力して360度対応できるためこちらがよく使われるみたいです。
（説明が正確ではないかも‥詳しくはググってみてください）
入力ポートの並び順がシェーダーの引数と同じように「Y」「X」の順になっているので差し間違えないご注意を（UE4標準のマテリアル関数内ではCustomノードでAtan2を記述して使用している場合があり、そちらは「X」「Y」の順になってたりするのでこちらも注意）。
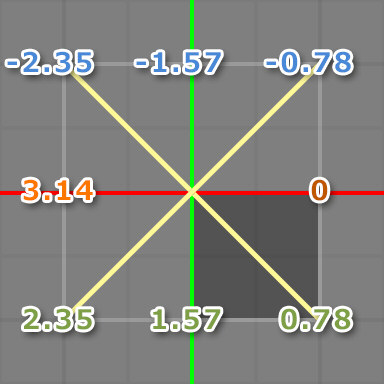
Arctangent2 にUVを与えると下図のような結果になります。
後半の180度はVがマイナス値になっているため結果もマイナスになっています。
X軸でミラー反転させたような感じですね。
また、360度のような「度数」ではなくラジアンの値になるため、丁度180度が3.14になっています。
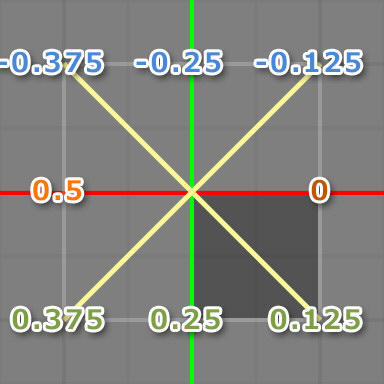
次にDivideの部分について。
360度は2パイラジアンなので、3.14..の倍の 6.28..で割っています。
これはつまり、値を正規化するイメージですね。
するとこちらのように180度が 0.5 と「0～1」の範囲になりました。
ただしマイナス側の値がこのままでは問題があります。
そこで最後に Frac を通してやると、結果 0～360度が綺麗に 0～1 の範囲になりました。
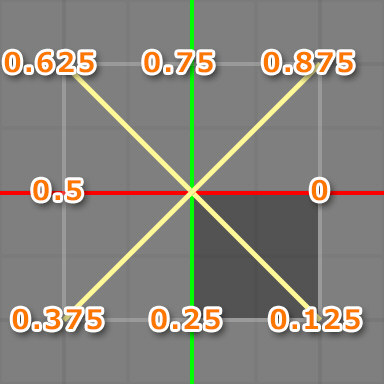
Frac は普段は正の値に対して使うことが多いので「小数点だけ取り出す」ものというイメージでしたが、実際のところはもうちょっと複雑みたいです。
UE4の公式ドキュメントによると下記のように説明されています。
受け取った値の端数部分を出力します。
言い換えると、入力値が "X" の場合、結果は "X - X の Floor" です。
ややこしいですが「-0.2」を与えると「0.8」が返り、「-1.6」を与えると「0.4」が返る‥といった感じのようです。
これで見事にぐるりと極座標に展開できています。面白い！
